Sponsored By

Our Partners
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |


Indian Institute of Technology Madras is one of the leading globally significant institutes of higher technical education, fundamental and applied science and research. The field of “Quantum Technology” is one of the cutting-edge research areas that IITM seeks to explore and this has led to the birth of our new Center for Quantum Information, Communication and Computing.
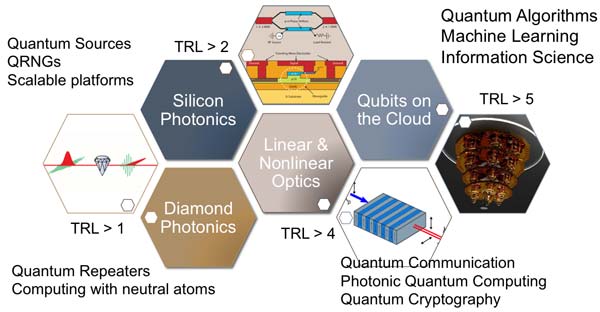
The Center is set up with an objective of developing various facets of various applications of quantum technologies in the area of secure quantum communications, including quantum key delivery, quantum random number generation, quantum sensing and metrology, as well as quantum computing-related innovations.
Sponsored By

Our Partners
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |